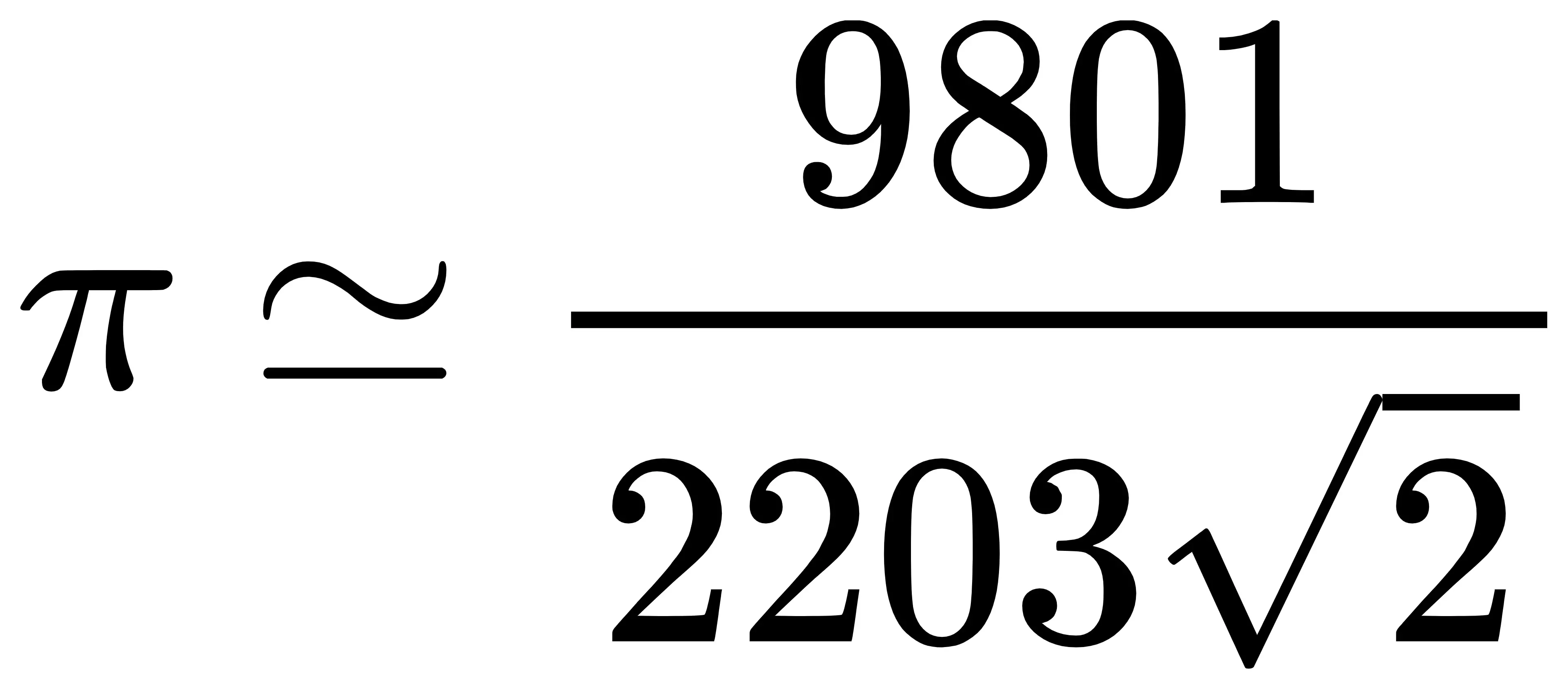正项级数收敛性的判别方法

正项级数是指级数中所有项都是非负数的级数。对于正项级数的收敛性，我们有以下判别方法：

1. 比较法：对于两个级数 $\sum_{n=1}^{\infty}a_n$ 和 $\sum_{n=1}^{\infty}b_n$，如果存在正整数 $N$，使得当 $n\ge N$ 时，$a_n\le b_n$，那么如果级数 $\sum_{n=1}^{\infty}b_n$ 收敛，那么级数 $\sum_{n=1}^{\infty}a_n$ 也收敛；如果级数 $\sum_{n=1}^{\infty}b_n$ 发散，那么级数 $\sum_{n=1}^{\infty}a_n$ 也发散。

2. 极限比较法：如果存在正整数 $N$，使得当 $n\ge N$ 时，$0\le \frac{a_n}{b_n}\le K$，其中 $K$ 是一个常数，那么级数 $\sum_{n=1}^{\infty}b_n$ 和级数 $\sum_{n=1}^{\infty}a_n$ 要么同时收敛，要么同时发散。

3. 极限根值法：对于正项级数 $\sum_{n=1}^{\infty}a_n$，如果 $\lim_{n\to\infty}\sqrt[n]{a_n}=L$，那么当 $L<1$ 时，级数 $\sum_{n=1}^{\infty}a_n$ 收敛；当 $L>1$ 时，级数 $\sum_{n=1}^{\infty}a_n$ 发散；当 $L=1$ 时，判别不出级数的收敛性。

4. 积分判别法：对于单调递减的正函数 $f(x)$，如果 $\int_{1}^{\infty}f(x)\mathrm{d}x$ 收敛，那么级数 $\sum_{n=1}^{\infty}f(n)$ 收敛；如果 $\int_{1}^{\infty}f(x)\mathrm{d}x$ 发散，那么级数 $\sum_{n=1}^{\infty}f(n)$ 发散。

以上就是正项级数收敛性的四种判别方法，它们在实际计算中都有所应用。需要注意的是，这些方法只适用于正项级数，对于一般的级数，我们需要用到更为复杂的方法进行分析。